
- Science Toys
- Magnetism
- Electromagnetism
- Electrochemistry
- Radio
- Thermodynamics
- Aerodynamics
- Light and optics
- Simple laser communicator
- Make your own 3D pictures
- Making permanent rainbows.
- A solar powered marshmallow roaster
- Make a spectroscope from a CD.
- The impossible kaleidoscope
- Make a solar hotdog cooker
- Exploring invisible light
- A high resolution spectrograph.
- Time-lapse photography.
- High speed photography.
- Stacking photos for high depth of field.
- Biology
- Mathematics
- Computers and Electronics
Calculating the strength of a magnet
We're going to start with an electromagnet, to look at how magnets are measured, because in some ways it is easier to understand electromagnets first.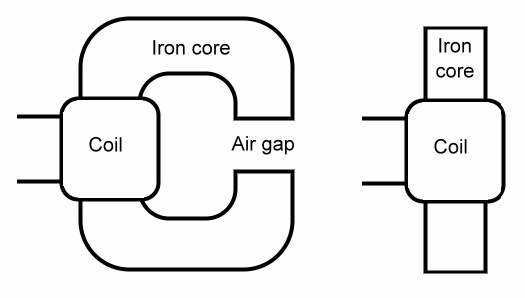 Consider the two electromagnets shown above. The one on the right is a simple
coil of insulated copper wire wound around a piece of iron, such as a nail.
The one on the left is the same, but the iron core has been bent around into
the shape of the letter 'C', much like a horseshoe magnet.
The left picture makes it easier to see what is called a magnetic circuit.
The coil makes a magnet that has a north and a south pole, and the magnetism
moves in a circuit from the north to the south, crossing the air gap to get there.
In this respect, a magnetic circuit is similar to an electrical circuit. The flow always
goes from one pole to another, like electricity goes from one side of a battery
to the other.
Magnetic flux is reluctant to travel through air. It is much easier for it to travel
through iron. We say that air has a high reluctance, and iron has a low
reluctance. This is similar to resistance in an electrical circuit.
In an electrical circuit, we have Ohm's Law, which says that voltage is equal to
current times resistance. In a similar way, magnetomotive force is equal to the
magnetic flux times the reluctance. Thus magnetomotive force is similar to voltage,
and magnetic flux is similar to current.
The magnetomotive force is produced by the coil. It is measured in ampere-turns,
the electrical current in the coil, measured in amperes, times the number of
turns of wire in the coil.
We can calculate the reluctance of the iron core and the air gap if we know the
length, the area, and the permeability of the iron and the air. Just like
in calculating the resistance of a wire, the reluctance goes down if the cross
sectional area gets bigger, and the reluctance goes up if the length gets longer.
The permeability is a constant that depends on the material.
The permeability of free space, also known as the magnetic constant,
is 0.00000125663706 meters kilograms seconds-2 amperes-2.
Rather than remember all of those clumsy units, we have a simpler unit, the henry,
and we measure permeability in henries per meter.
For simplicity, we will refer to permeability as the Greek letter "mu" μ, and
the permeability of free space as "mu sub zero", μ0, and say that air is 1 μ0
and iron is about 1,000 μ0.
The formula for reluctance is the length divided by the product of the permeability and the area.
We have an iron core that is one centimeter square in area, and is 15 centimeters
long, bent into a 'C' shape with a 1 centimeter air gap. The reluctance of the iron core is
15 centimeters divided by 1,000 times one square centimeter.
The reluctance of the air gap is 1 centimeter divided by 1 times 1 square centimeter.
We add the two together to get the reluctance of the entire magnetic circuit.
The iron core comes to
about 1.5
henries per meter, and the air gap comes to
about 100.
Now we can calculate the magnetic flux in our magnetic circuit. Flux is measured in Webers.
Suppose we have just one loop in our coil, and we have 1 ampere of current going through the coil.
We thus have 1 ampere-turn of magnetomotive force.
Dividing one ampere by the total reluctance of the circuit, we get
0.0000000123806607 webers.
That is the total flux. We also measure the flux density, that is, the flux per square meter (called B).
Webers per square meter is a unit known as the tesla. We have
0.000123806607 teslas in the air gap of our our one-turn electromagnet.
If we had 5,000 turns of wire in our coil, we would have 5,000 times the flux density, or
0.619033035 teslas in the air gap of our our 5,000-turn electromagnet.
Our little 'C' shaped magnet has room for a coil about 3 centimeters long and 4 centimeters wide.
If we use 28 gauge wire (0.33 millimeters in diameter), we can get about 90 turns per layer, and
about 120 layers, for a total of about 10,000 turns. 28 gauge wire can handle 1.4 amperes of
current (more if we cool the coil with water or liquid helium).
So, our magnet is now up to
1.7 teslas, and runs very hot.
The average length of one turn of wire in our coil is about 10 centimeters. We have 10,000 turns, so
that is one kilometer of wire. A kilometer of 28 gauge wire has 213 ohms of resistance. To get
1.4 amperes through 213 ohms of resistance takes
just under 300 volts.
We have calculated flux and flux density of our coil. Now we need the magnetic field strength.
We start with the magnetomotive force we discussed earlier, which is simply the number of ampere-turns
in our coil. We have 1.4 amperes, and 10,000 turns, so we have 14,000 ampere-turns of magnetomotive
force. The magnetic field strength is the magnetomotive force divided by the length of the
magnetic circuit, which in our example is 16 centimeters. So the magnetic field strength (called H)
is 14,000 ampere-turns/16 centimeters, or 875 ampere-turns per centimeter.
So far we have been discussing the 'C' shaped magnet. The simpler magnet works the same way,
but the length of the iron core is now 8 centimeters, and the length of the air gap has increased
considerably.
If we assume for the moment that the air gap is now the same length as the iron core (each is now 8 centimeters), we get
0.22
teslas, and it still runs very hot. The magnetomotive force has not changed (still 14,000 ampere-turns),
but the flux has dropped considerably, since the extra 7 centimeters of air gap has a lot more reluctance.
However, the air gap is actually larger than 8 centimeters. The magnetic flux in the iron stays pretty much
entirely in the iron. This is because up to the saturation point of the iron, it is a very good conductor
of magnetic flux. Air, on the other hand, is a poor conductor, and the flux spreads out over a large area,
making the average path length larger.
Permanent magnets have the same units of strength and flux. A permanent magnet with a flux density of
1.32 tesla (such as an N42 neodymium-iron-boron magnet) has the same flux density as our 'C' shaped
magnet if we reduce the current to
1.067 amperes.
The same permanent magnet has a magnetic field strength of 11,000 ampere-turns per centimeter.
This is 12.5 times as strong as our electromagnet. We would need to add more current or
more windings, or reduce the length of the magnetic circuit to get the same strength as the permanent magnet.
Of course, we could do some combination of the three.
In a practical electromagnet, this is difficult. Reducing the length of the circuit means that there will
be less room for the coil. Adding turns means we need a longer magnetic circuit to hold them. Adding
current means that we need a fatter wire, which means we get fewer turns in the same space. You can see
why people choose to cool their electromagnets with water or cryogenic liquids. It allows you to use
more current without increasing the diameter of the wire.
What the magnetic field strength means in terms of our permanent magnet is simple.
It is the strength of an electromagnet needed to demagnetize the permanent magnet.
Consider the two electromagnets shown above. The one on the right is a simple
coil of insulated copper wire wound around a piece of iron, such as a nail.
The one on the left is the same, but the iron core has been bent around into
the shape of the letter 'C', much like a horseshoe magnet.
The left picture makes it easier to see what is called a magnetic circuit.
The coil makes a magnet that has a north and a south pole, and the magnetism
moves in a circuit from the north to the south, crossing the air gap to get there.
In this respect, a magnetic circuit is similar to an electrical circuit. The flow always
goes from one pole to another, like electricity goes from one side of a battery
to the other.
Magnetic flux is reluctant to travel through air. It is much easier for it to travel
through iron. We say that air has a high reluctance, and iron has a low
reluctance. This is similar to resistance in an electrical circuit.
In an electrical circuit, we have Ohm's Law, which says that voltage is equal to
current times resistance. In a similar way, magnetomotive force is equal to the
magnetic flux times the reluctance. Thus magnetomotive force is similar to voltage,
and magnetic flux is similar to current.
The magnetomotive force is produced by the coil. It is measured in ampere-turns,
the electrical current in the coil, measured in amperes, times the number of
turns of wire in the coil.
We can calculate the reluctance of the iron core and the air gap if we know the
length, the area, and the permeability of the iron and the air. Just like
in calculating the resistance of a wire, the reluctance goes down if the cross
sectional area gets bigger, and the reluctance goes up if the length gets longer.
The permeability is a constant that depends on the material.
The permeability of free space, also known as the magnetic constant,
is 0.00000125663706 meters kilograms seconds-2 amperes-2.
Rather than remember all of those clumsy units, we have a simpler unit, the henry,
and we measure permeability in henries per meter.
For simplicity, we will refer to permeability as the Greek letter "mu" μ, and
the permeability of free space as "mu sub zero", μ0, and say that air is 1 μ0
and iron is about 1,000 μ0.
The formula for reluctance is the length divided by the product of the permeability and the area.
We have an iron core that is one centimeter square in area, and is 15 centimeters
long, bent into a 'C' shape with a 1 centimeter air gap. The reluctance of the iron core is
15 centimeters divided by 1,000 times one square centimeter.
The reluctance of the air gap is 1 centimeter divided by 1 times 1 square centimeter.
We add the two together to get the reluctance of the entire magnetic circuit.
The iron core comes to
about 1.5
henries per meter, and the air gap comes to
about 100.
Now we can calculate the magnetic flux in our magnetic circuit. Flux is measured in Webers.
Suppose we have just one loop in our coil, and we have 1 ampere of current going through the coil.
We thus have 1 ampere-turn of magnetomotive force.
Dividing one ampere by the total reluctance of the circuit, we get
0.0000000123806607 webers.
That is the total flux. We also measure the flux density, that is, the flux per square meter (called B).
Webers per square meter is a unit known as the tesla. We have
0.000123806607 teslas in the air gap of our our one-turn electromagnet.
If we had 5,000 turns of wire in our coil, we would have 5,000 times the flux density, or
0.619033035 teslas in the air gap of our our 5,000-turn electromagnet.
Our little 'C' shaped magnet has room for a coil about 3 centimeters long and 4 centimeters wide.
If we use 28 gauge wire (0.33 millimeters in diameter), we can get about 90 turns per layer, and
about 120 layers, for a total of about 10,000 turns. 28 gauge wire can handle 1.4 amperes of
current (more if we cool the coil with water or liquid helium).
So, our magnet is now up to
1.7 teslas, and runs very hot.
The average length of one turn of wire in our coil is about 10 centimeters. We have 10,000 turns, so
that is one kilometer of wire. A kilometer of 28 gauge wire has 213 ohms of resistance. To get
1.4 amperes through 213 ohms of resistance takes
just under 300 volts.
We have calculated flux and flux density of our coil. Now we need the magnetic field strength.
We start with the magnetomotive force we discussed earlier, which is simply the number of ampere-turns
in our coil. We have 1.4 amperes, and 10,000 turns, so we have 14,000 ampere-turns of magnetomotive
force. The magnetic field strength is the magnetomotive force divided by the length of the
magnetic circuit, which in our example is 16 centimeters. So the magnetic field strength (called H)
is 14,000 ampere-turns/16 centimeters, or 875 ampere-turns per centimeter.
So far we have been discussing the 'C' shaped magnet. The simpler magnet works the same way,
but the length of the iron core is now 8 centimeters, and the length of the air gap has increased
considerably.
If we assume for the moment that the air gap is now the same length as the iron core (each is now 8 centimeters), we get
0.22
teslas, and it still runs very hot. The magnetomotive force has not changed (still 14,000 ampere-turns),
but the flux has dropped considerably, since the extra 7 centimeters of air gap has a lot more reluctance.
However, the air gap is actually larger than 8 centimeters. The magnetic flux in the iron stays pretty much
entirely in the iron. This is because up to the saturation point of the iron, it is a very good conductor
of magnetic flux. Air, on the other hand, is a poor conductor, and the flux spreads out over a large area,
making the average path length larger.
Permanent magnets have the same units of strength and flux. A permanent magnet with a flux density of
1.32 tesla (such as an N42 neodymium-iron-boron magnet) has the same flux density as our 'C' shaped
magnet if we reduce the current to
1.067 amperes.
The same permanent magnet has a magnetic field strength of 11,000 ampere-turns per centimeter.
This is 12.5 times as strong as our electromagnet. We would need to add more current or
more windings, or reduce the length of the magnetic circuit to get the same strength as the permanent magnet.
Of course, we could do some combination of the three.
In a practical electromagnet, this is difficult. Reducing the length of the circuit means that there will
be less room for the coil. Adding turns means we need a longer magnetic circuit to hold them. Adding
current means that we need a fatter wire, which means we get fewer turns in the same space. You can see
why people choose to cool their electromagnets with water or cryogenic liquids. It allows you to use
more current without increasing the diameter of the wire.
What the magnetic field strength means in terms of our permanent magnet is simple.
It is the strength of an electromagnet needed to demagnetize the permanent magnet.

Send mail to Simon Quellen Field via sfield@scitoys.com