
- Science Toys
- Magnetism
- Electromagnetism
- Electrochemistry
- Radio
- Thermodynamics
- Aerodynamics
- Light and optics
- Simple laser communicator
- Make your own 3D pictures
- Making permanent rainbows.
- A solar powered marshmallow roaster
- Make a spectroscope from a CD.
- The impossible kaleidoscope
- Make a solar hotdog cooker
- Exploring invisible light
- A high resolution spectrograph.
- Time-lapse photography.
- High speed photography.
- Stacking photos for high depth of field.
- Biology
- Mathematics
- Computers and Electronics
Cook hotdogs with the Sun in minutes.
In this section we will show you how to make a powerful solar concentrator that can cook four or five hotdogs in minutes. The Solar Hotdog Cooker is made out of a thin (1/8 inch thick)
plastic mirror that can be found at plastic shops and glass
stores (although it may have to be special ordered at some
stores). The plastic is bent into the shape of a parabola,
so that the sun's rays are collected over an eight square foot
area, and focused in a thin line. The hotdogs are roasted on
a spit placed at the focus, and turned every once in a while
to prevent them from burning.
The Solar Hotdog Cooker is made out of a thin (1/8 inch thick)
plastic mirror that can be found at plastic shops and glass
stores (although it may have to be special ordered at some
stores). The plastic is bent into the shape of a parabola,
so that the sun's rays are collected over an eight square foot
area, and focused in a thin line. The hotdogs are roasted on
a spit placed at the focus, and turned every once in a while
to prevent them from burning.

Click on picture to see a larger image
Materials
For the solar cooker you will need:- Two pieces of plywood, 1/2 inch thick, 2 feet wide and 4 feet long.
- Two pieces of lumber, (2x4) 1 1/2 inch thick, 3 1/2 inch wide, and 8 feet long.
- 16 wood screws, 2 inches long.
- One stiff steel wire, 3 feet long.
- 92 small nails or wooden pegs, about an inch long.
- One plastic mirror, 1/8 inch thick, 2 feet wide, 6 feet long (although 5 1/2 feet long might work better).
- A drill and a bit that matches the diameter of the 92 small nails or pegs. A larger bit (over 1 inch wide) is needed for the food hole.
Assembly
Place the two sheets of plywood together, one on top of the other. Using a tape measure and a carpenter's square, mark off where the holes will be drilled for the mirror supports (the 92 small nails or pegs). All holes are drilled completely through both sheets of plywood. The holes are to be drilled according to the following table:
|
Spacing for drilled holes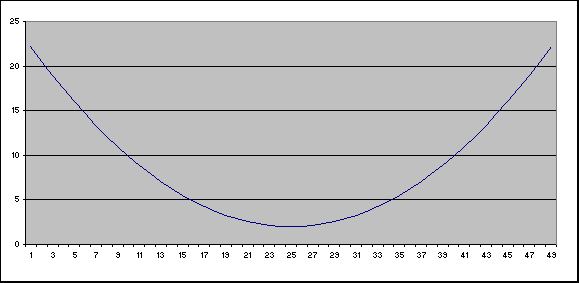
A second row of holes is drilled above these, separated by the thickness of the mirror. |

Click on picture to see a larger image The photo above shows the back side of the cooker, where the 2x4 spreaders can be seen. Note also the remaining length of 2x4 is used as a support (more about that later). Next push 46 of the small nails into the bottom row of holes. Now set the mirror onto the top of the cooker, and gently push it down to rest on the nails. Put a pair of nails in the center pair of holes on top of the mirror, then work your way outwards, placing pairs of nails to hold the mirror down. (I used cotton tipped wooden swabs in the picture because they photograph better than nails.) The last step is to place a few screws in the remaining long piece of 2x4, leaving the head of the screws sticking an inch or two out of the wood. These will act as supports to hold the cooker so it is tilted toward the sun. The spit is formed from the 3 foot piece of wire. A coat hanger can be used, but wires that thin tend to sag in the middle when burdened by a few hotdogs. A thicker, stiffer wire is better. To make it easier to turn the food, a crank is formed by bending the wire at one end as shown in the labeled photo.
Cooking with the sun
Carefully poke the 3 foot wire spit through the hotdogs or kebabs. Try to center the food on the spit, so the food will rotate when you rotate the spit, instead of slipping to keep the heavy part down. Insert the spit through the food hole, and insert the far end of the wire into the small focus hole in the far plywood sheet. Rest the near end of the spit in the small focus hole at the bottom of the food hole. Align the solar cooker with the sun. Start with the cooker flat on the ground, then turn it until it is parallel with your shadow. The sun will just barely graze both of the plywood sheets when the cooker is aligned properly (this can be seen in most of the photos on this page). Next tip one end of the cooker up until the shadow of the spit falls directly on the center nail at the bottom of the parabola. This can be clearly seen in the labeled photo. Hold the remaining scrap of 2x4 up against the back side of the cooker, and mark where a screw should be placed to hold the cooker at the right elevation. Screw the screw into the 2x4, leaving an inch or two sticking out to hold the top 2x4 spreader. If you like, the screw can be placed a little higher up, and the cooker can be adjusted to the exact angle by tilting the support backwards.
Click on picture to see a larger image When the cooker is adjusted properly, the sun will be focused on the food, making bright lines across it (sunglasses are recommended at this phase). You can see the shadows of the nails on the walls of the cooker. These shadows should all cross at the focus, where the hotdogs are. The hotdogs can be seen in the mirror, highly magnified. The shadow of the hotdogs can be seen being cast by the mirror onto the back side of the hotdogs in the photo above. In the photo below, the shadows of the nails can be clearly seen, crossing at the focus of the parabola.

Click on picture to see a larger image The hotdogs will start steaming in less than a minute. The spit should be turned every couple minutes to prevent black lines from being burned into the food (unless you like your hotdogs with black stripes). The hotdogs will be quite hot in about 10 minutes, or burned black all over in about 20 minutes.

Click on picture to see a larger image Things to notice in the above photo:
- The shadows of the mirror supports seem to meet at the focus.
- The shadow of the hotdogs is projected onto the enlarged reflection of the hotdogs.
- The enlargement of the hotdogs only occurs in their width, not their length, because the mirror is only curved in one dimension.
- The poor hotdogs have been burned to a crisp (oops...).
How does it do that?
A parabola is a shape with some interesting properties that make it perfect for cooking hotdogs. The sun is bigger than the earth, and very far away. This means that the sunlight that hits the earth appears to be in parallel rays. If we had thousands of tiny mirrors, connected by hinges in a line, and we tilted each mirror so it would reflect these parallel rays onto one spot, the mirrors would line up in a parabola. Mathematically, a parabola is defined as a set of points that are
the same distance from both a point (called the focus) and a straight
line (called the directrix).
Mathematically, a parabola is defined as a set of points that are
the same distance from both a point (called the focus) and a straight
line (called the directrix).
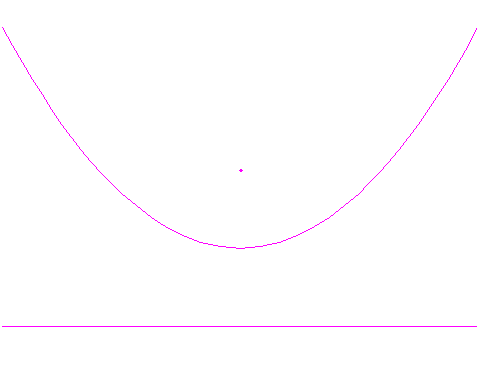 The formula for the parabola used in the solar cooker is
The formula for the parabola used in the solar cooker is
y = 0.035x2+2
I chose this formula so the parabola would be deeply curved, and would fit
into the 2 foot by 4 foot plywood sheets. We want the focus to be close
to the mirror, so that as the sun moves, the focus does not move very
much.
Having the focus close to the mirror is like having the fulcrum
of a lever close to one end. The sun end of our lever can move a lot,
while the hotdog end of our lever hardly moves at all. This means that
we don't have to raise or lower the cooker very often as the sun moves.
The +2 part of the equation says that the bottom of the parabola will
be 2 inches from the bottom of the plywood. This gives us room for
the 2x4 spreaders, and room to drill the bottom hole for the support
nails.
The bottom of the parabola is called the vertex. The vertex is always
halfway between the focus and the directrix. The distance from the
vertex to the focus is
1
0.035
4
or about 7.14 inches.
A square meter of the earth's surface gets about 1000 watts of power
from sunlight. Our mirror intercepts about 8 square feet of sunlight,
or about three quarters of a square meter. This means that our cooker
is the rough equivalent of a 750 watt electric stove.
Next: Exploring invisible light
Del.icio.us
0.035
4
- Science Toys
- Magnetism
- Electromagnetism
- Electrochemistry
- Radio
- Thermodynamics
- Aerodynamics
- Light and optics
- Simple laser communicator
- Make your own 3D pictures
- Making permanent rainbows.
- A solar powered marshmallow roaster
- Make a spectroscope from a CD.
- The impossible kaleidoscope
- Make a solar hotdog cooker
- Exploring invisible light
- A high resolution spectrograph.
- Time-lapse photography.
- High speed photography.
- Stacking photos for high depth of field.
- Biology
- Mathematics
- Computers and Electronics
Some of my other web sites:

Send mail to Simon Quellen Field via sfield@scitoys.com