|
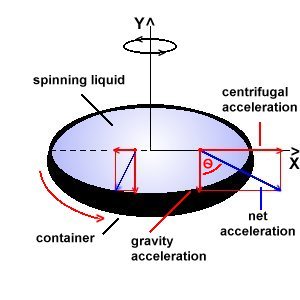
J. Surdej and A. Pospieszalska-Surdej What is a liquid mirror? As we all know, a perfect reflecting parabola represents the ideal contour for a mirror to focus parallel rays of light into a single point. It is therefore of the greatest importance to have realized that a rotating liquid surface takes the shape of a parabola under the constant pull of gravity and a centrifugal acceleration, which grows stronger as the distance from the central axis increases (E. Cappoci, 1850). The parabolic shape occurs because a liquid surface always sets it local surface perpendicular to the net acceleration it experiences, which in this case becomes stronger and less inclined with distance from the central axis (see Figure 1).
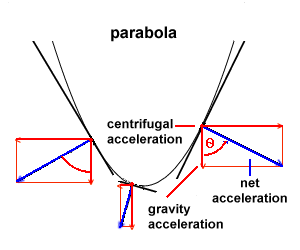
Indeed, inspection of the above figure clearly shows that the tangent dy/dx to the liquid surface may be expressed as (see Figure 2) dy/dx = tg( where y = which, by analogy with the equation of a parabola caracterized by the focal length f, i.e. y = x2/(4f), (3) implies that the focal length of the liquid mirror is merely given by the relation f = g/(2 A focal length of approximately 40 cm is obtained for a value of the angular velocity of 33 turns per minute. "Home-made" liquid mirror telescope A gramophone with a turntable of 20 cm in diameter may thus provide us with a perfect liquid mirror characterized by a focal ratio f/D ~ 2, a very acceptable value for an astronomical mirror. For large mirrors of practical interest, the periods of rotation are typically of the order of several seconds and the linear velocities at the rims of the mirrors range between 2 and 10 km/h, very near the velocity of a walking man. It is very instructive to construct a small size liquid mirror by pouring in a small cylindrical container, set on the turntable of a gramophone, some polyurethane. After polimerisation of this resine, in the form of a pre-shaped paraboloid, one may conveniently fill the latter with some used car oil (or mercury in the case of a real astronomical mirror). By means of a small eyepiece set at the focus of the spinning paraboloid, it then becomes possible to observe distant objects located just above the gramophone (see Figure 3). More professional liquid mirrors have been constructed at various locations. 
Figure 3: "Home-made" liquid mirror telescope: Cylindrical container, set on the turntable of a gramophone filled with oil
|
|||||||||
 ) =
) =  2x / g,
(1)
2x / g,
(1)
